Important Links:

Arxiv: https://arxiv.org/abs/1901.03707

Github: https://github.com/dgilton/neumann_networks_code

Neumann Networks

The Neumann Network is a method of solving ill-posed linear inverse problems by learning a nonlinear regularizer, in the form of a deep neural network. Examples of some such ill-posed linear inverse problems are deblurring, inpainting, compressed sensing, undersampled MRI reconstruction, deconvolution, superresolution, and more.

Typically these problems are solved by solving the following problem, where the solution must both be able to reproduce the original measurements (data-consistency) and have some desirable structure (regularization).

The Neumann series estimator that solves this problem (for quadratic regularizer r() ) is:

A visualization of the resulting computational graph is here:

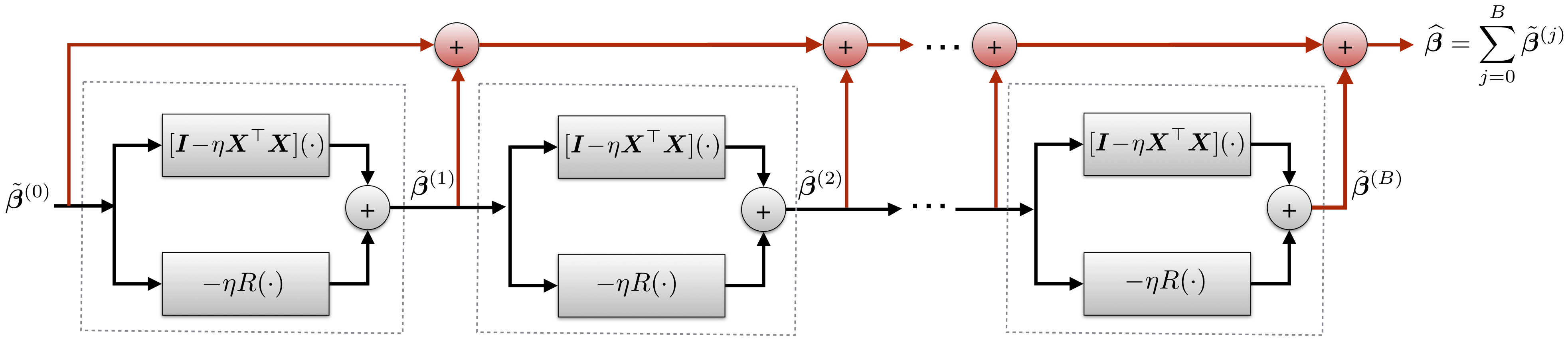
By replacing R() with a deep neural network, we can leverage training data to train the entire network end-to-end, similar to existing unrolled iterative methods. The resulting Neumann network is not motivated by an existing optimization algorithm, permitting novel analysis and empirical benefits.

Note that the Neumann series identity used to create the above estimator is not valid in general for nonlinear regularizers. However, we demonstrate for data drawn from a union of subspaces and piecewise linear regularizer (satisfied by a neural network with ReLU activations) there is an optimal reconstruction that has identical form to the Neumann series above.

The red lines on the above diagram denote long-ranging residual connections, which arise naturally through the structure of our estimator. We hypothesize these residual connections result in a more favorable optimization landscape than more traditional iterative methods. These improvements are especially noticeable in the case of small datasets.

Results

We have run experiments for reconstruction tasks on subsets of the Cifar10, CelebA, and STL10 datasets. In addition, we demonstrate the potential of the Neumann network for undersampled MRI reconstruction by testing on the dataset gathered by Aggarwal et. al (2018); access their arxiv paper here.

MRI Reconstruction

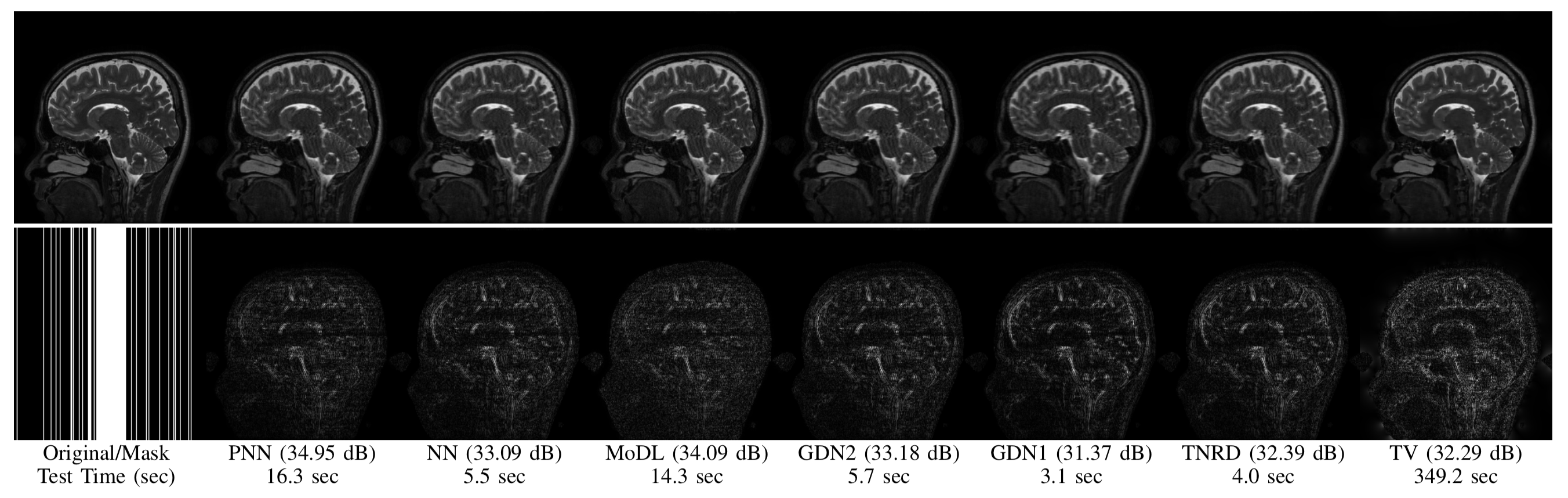
Top row: Original image and reconstructions given by several methods. Bottom row: Image mask and

CelebA Deblurring

From left to right, top row: Original image, Neumann Network reconstruction, Gradient Descent Network reconstruction, and single residual network reconstruction.
Bottom row: Input to the networks, followed by residual images multiplied by 6x for improved visualization.

STL10 Compressed Sensing

From left to right, top row: Original image, Neumann Network reconstruction, Gradient Descent Network reconstruction, and single residual network reconstruction. Bottom row: Input to the networks, followed by residual images multiplied by 6x for improved visualization.

Preconditioning

It is straightforward to incorporate arbitrary preconditioning operators into the Neumann Network architecture. The below graphic demonstrates the altered architecture, where T() is the preconditioner. On certain types of ill-conditioned forward operators, this preconditioning step can considerably improve performance.

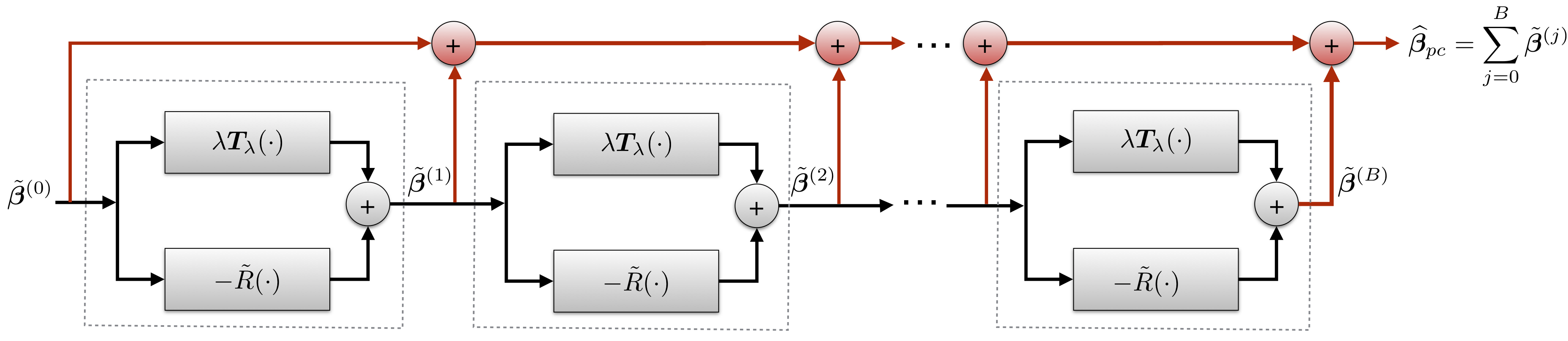
The main differences between the preconditioned version and vanilla Neumann Network is in the data-consistency term of each block, which has been replaced by a preconditioning operator, and the initialization, which has been replaced by a preconditioned initial estimate.

Dependencies

This code has been tested on the following:

Tensorflow: 1.13.1
Python: 3.7.3 (But most modern 3.6 should be fine too)
Cuda: 9.0

If you experience issues, please contact the corresponding author via email or submit an issue. Be especially careful that your Tensorflow version is the same as listed. I highly recommend installing Tensorflow via conda in a virtualenv.

Using the code

Documentation for the code and instructions for training and testing are on the Github repo.

If you have questions, requests, ideas, or are interested in a resource that is not provided here or on the Github (like a pretrained checkpoint for a problem or method) please contact Davis Gilton via email. His email is his last name at wisc.edu .

To Do: Downloadable checkpoints. Repository for comparison methods in Tensorflow.

---